Shortest Path in AQL

Find one path of shortest length between two nodes

General query idea

This type of query finds the shortest path between two given documents (startNode and endNode) in your graph. If there are multiple shortest paths, the path with the lowest weight or a random one (in case of a tie) is returned.

The shortest path search emits the following two variables for every step of the path:

The node on this path.
The edge pointing to it.

Example execution

Let’s take a look at a simple example to explain how it works. This is the graph that you are going to find a shortest path on:

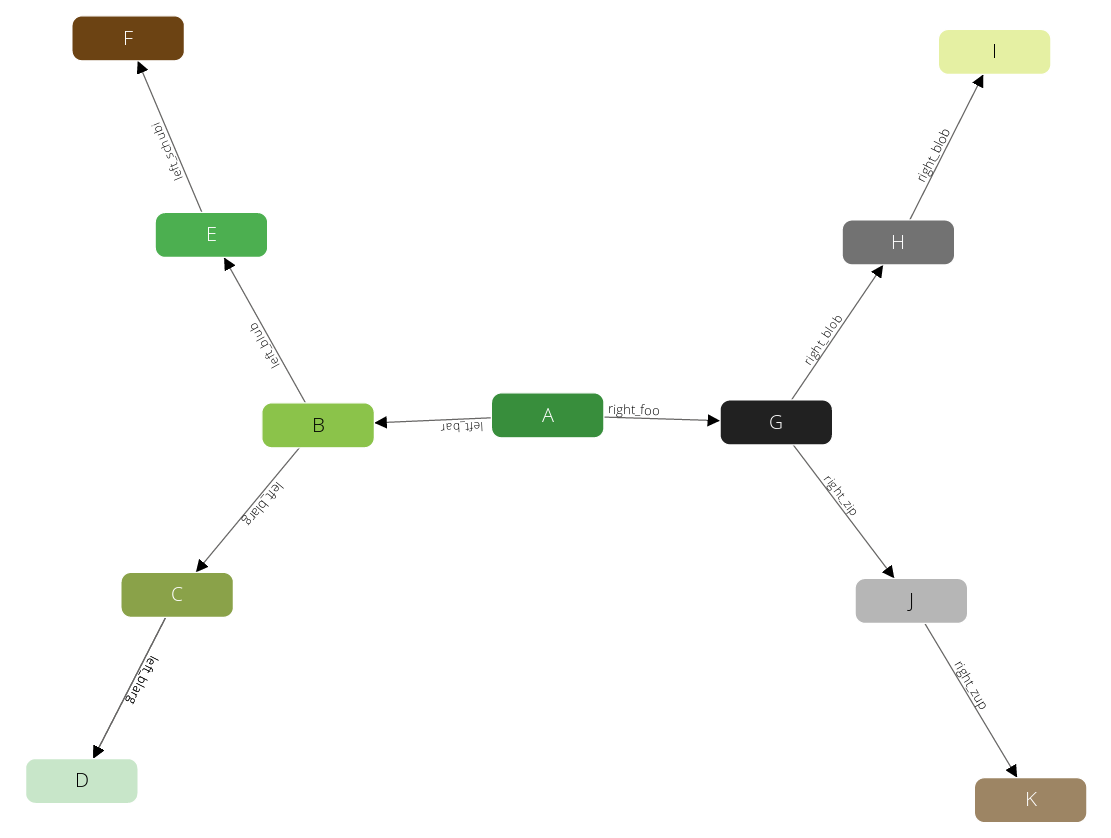
traversal graph

You can use the following parameters for the query:

You start at the node A.
You finish with the node D.

So, obviously, you have the nodes A, B, C and D on the shortest path in exactly this order. Then, the shortest path statement returns the following pairs:

Node	Edge
A	null
B	A → B
C	B → C
D	C → D

Note that the first edge is always null because there is no edge pointing to the startNode.

Syntax

The next step is to see how you can write a shortest path query. You have two options here, you can either use a named graph or a set of edge collections (anonymous graph).

Working with named graphs

FOR node[, edge]
  IN OUTBOUND|INBOUND|ANY SHORTEST_PATH
  startNode TO endNode
  GRAPH graphName
  [OPTIONS options]

FOR: Emits up to two variables:
- node (object): The current node on the shortest path
- edge (object, optional): The edge pointing to the node
IN OUTBOUND|INBOUND|ANY: Defines in which direction edges are followed (outgoing, incoming, or both)
startNode TO endNode (both string|object): The two nodes between which the shortest path is computed. This can be specified in the form of an ID string or in the form of a document with the attribute _id. All other values lead to a warning and an empty result. If one of the specified documents does not exist, the result is empty as well and there is no warning.
GRAPH graphName (string): The name identifying the named graph. Its node and edge collections are looked up for the path search.
OPTIONS options (object, optional): See the path search options.

Shortest Path traversals do not support negative weights. If a document attribute (as specified by weightAttribute) with a negative value is encountered during traversal, or if defaultWeight is set to a negative number, then the query is aborted with an error.

Working with collection sets

FOR node[, edge]
  IN OUTBOUND|INBOUND|ANY SHORTEST_PATH
  startNode TO endNode
  edgeCollection1, ..., edgeCollectionN
  [OPTIONS options]

Instead of GRAPH graphName you may specify a list of edge collections (anonymous graph). The involved node collections are determined by the edges of the given edge collections. The rest of the behavior is similar to the named version.

Path search options

You can optionally specify the following options to modify the execution of a graph path search. If you specify unknown options, query warnings are raised.

`weightAttribute`

A top-level edge attribute that should be used to read the edge weight (string).

If the attribute does not exist or is not numeric, the defaultWeight is used instead.

The attribute value must not be negative.

`defaultWeight`

This value is used as fallback if there is no weightAttribute in the edge document, or if it’s not a number (number).

The value must not be negative. The default is 1.

`useCache`

Introduced in: v3.12.2

Whether to use the in-memory cache for edges. The default is true.

You can set this option to false to not make a large graph operation pollute the edge cache.

Traversing in mixed directions

For shortest path with a list of edge collections you can optionally specify the direction for some of the edge collections. Say for example you have three edge collections edges1, edges2 and edges3, where in edges2 the direction has no relevance, but in edges1 and edges3 the direction should be taken into account. In this case you can use OUTBOUND as general search direction and ANY specifically for edges2 as follows:

FOR node IN OUTBOUND SHORTEST_PATH
  startNode TO endNode
  edges1, ANY edges2, edges3

All collections in the list that do not specify their own direction use the direction defined after IN (here: OUTBOUND). This allows you to use a different direction for each collection in your path search.

Graph path searches in a cluster

Due to the nature of graphs, edges may reference nodes from arbitrary collections. Following the paths can thus involve documents from various collections and it is not possible to predict which are visited in a traversal. Which collections need to be loaded by the graph engine can only be determined at run time.

Use the WITH operation to specify the node collections you expect to be involved. This is required for traversals using collection sets in cluster deployments. Declare the collection of the start node as well if it’s not declared already (like by a FOR loop).

From v3.12.6 onward, node collections are automatically deduced for graph queries using collection sets / anonymous graphs if there is a named graph with a matching edge collection in its edge definitions.

For example, suppose you have two node collections, person and movie, and an acts_in edge collection that connects them. If you want to run a path search query that starts (and ends) at a person that you specify with its document ID, you need to declare both node collections at the beginning of the query:

WITH person, movie
FOR v IN ANY SHORTEST_PATH "person/1544" TO "person/52560" acts_in
  RETURN v.label

However, if there is a named graph that includes an edge definition for the acts_in edge collection, with person as the from collection and movie as the to collection, you can omit WITH person, movie. That is, if you specify acts_in as an edge collection in an anonymous graph query, all named graphs are checked for this edge collection, and if there is a matching edge definition, its node collections are automatically added as data sources to the query.

FOR v IN ANY SHORTEST_PATH "person/1544" TO "person/52560" acts_in
  RETURN v.label

// Chris Rock --> Dogma <-- Ben Affleck --> Surviving Christmas <-- Jennifer Morrison

You can still declare collections manually, in which case they are added as data sources in addition to automatically deduced collections.

Conditional shortest path

The SHORTEST_PATH computation only finds an unconditioned shortest path. With this construct it is not possible to define a condition like: “Find the shortest path where all edges are of type X”. If you want to do this, use a normal Traversal instead with the option {order: "bfs"} in combination with LIMIT 1.

Please also consider using WITH to specify the collections you expect to be involved.

Examples

Creating a simple symmetric traversal demonstration graph:

traversal graph

var examples = require("@arangodb/graph-examples/example-graph");
var graph = examples.loadGraph("traversalGraph");
db.circles.toArray();
db.edges.toArray();

Show output

[ 
  { 
    "_key" : "A", 
    "_id" : "circles/A", 
    "_rev" : "_kgUtVcm---", 
    "label" : "1" 
  }, 
  { 
    "_key" : "B", 
    "_id" : "circles/B", 
    "_rev" : "_kgUtVcm--_", 
    "label" : "2" 
  }, 
  { 
    "_key" : "C", 
    "_id" : "circles/C", 
    "_rev" : "_kgUtVcm--A", 
    "label" : "3" 
  }, 
  { 
    "_key" : "D", 
    "_id" : "circles/D", 
    "_rev" : "_kgUtVcq---", 
    "label" : "4" 
  }, 
  { 
    "_key" : "E", 
    "_id" : "circles/E", 
    "_rev" : "_kgUtVcq--_", 
    "label" : "5" 
  }, 
  { 
    "_key" : "F", 
    "_id" : "circles/F", 
    "_rev" : "_kgUtVcq--A", 
    "label" : "6" 
  }, 
  { 
    "_key" : "G", 
    "_id" : "circles/G", 
    "_rev" : "_kgUtVcq--B", 
    "label" : "7" 
  }, 
  { 
    "_key" : "H", 
    "_id" : "circles/H", 
    "_rev" : "_kgUtVcq--C", 
    "label" : "8" 
  }, 
  { 
    "_key" : "I", 
    "_id" : "circles/I", 
    "_rev" : "_kgUtVcq--D", 
    "label" : "9" 
  }, 
  { 
    "_key" : "J", 
    "_id" : "circles/J", 
    "_rev" : "_kgUtVcu---", 
    "label" : "10" 
  }, 
  { 
    "_key" : "K", 
    "_id" : "circles/K", 
    "_rev" : "_kgUtVcu--_", 
    "label" : "11" 
  } 
]

[ 
  { 
    "_key" : "65565", 
    "_id" : "edges/65565", 
    "_from" : "circles/A", 
    "_to" : "circles/B", 
    "_rev" : "_kgUtVcu--A", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "left_bar" 
  }, 
  { 
    "_key" : "65567", 
    "_id" : "edges/65567", 
    "_from" : "circles/B", 
    "_to" : "circles/C", 
    "_rev" : "_kgUtVcu--B", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "left_blarg" 
  }, 
  { 
    "_key" : "65569", 
    "_id" : "edges/65569", 
    "_from" : "circles/C", 
    "_to" : "circles/D", 
    "_rev" : "_kgUtVcu--C", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "left_blorg" 
  }, 
  { 
    "_key" : "65571", 
    "_id" : "edges/65571", 
    "_from" : "circles/B", 
    "_to" : "circles/E", 
    "_rev" : "_kgUtVcu--D", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "left_blub" 
  }, 
  { 
    "_key" : "65573", 
    "_id" : "edges/65573", 
    "_from" : "circles/E", 
    "_to" : "circles/F", 
    "_rev" : "_kgUtVcy---", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "left_schubi" 
  }, 
  { 
    "_key" : "65575", 
    "_id" : "edges/65575", 
    "_from" : "circles/A", 
    "_to" : "circles/G", 
    "_rev" : "_kgUtVcy--_", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "right_foo" 
  }, 
  { 
    "_key" : "65577", 
    "_id" : "edges/65577", 
    "_from" : "circles/G", 
    "_to" : "circles/H", 
    "_rev" : "_kgUtVcy--A", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "right_blob" 
  }, 
  { 
    "_key" : "65579", 
    "_id" : "edges/65579", 
    "_from" : "circles/H", 
    "_to" : "circles/I", 
    "_rev" : "_kgUtVcy--B", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "right_blub" 
  }, 
  { 
    "_key" : "65581", 
    "_id" : "edges/65581", 
    "_from" : "circles/G", 
    "_to" : "circles/J", 
    "_rev" : "_kgUtVcy--C", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "right_zip" 
  }, 
  { 
    "_key" : "65583", 
    "_id" : "edges/65583", 
    "_from" : "circles/J", 
    "_to" : "circles/K", 
    "_rev" : "_kgUtVcy--D", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "right_zup" 
  } 
]

Start with the shortest path from A to D as above:

db._query(`
  FOR v, e IN OUTBOUND SHORTEST_PATH 'circles/A' TO 'circles/D' GRAPH 'traversalGraph'
    RETURN [v._key, e._key]
`);

db._query(`
  FOR v, e IN OUTBOUND SHORTEST_PATH 'circles/A' TO 'circles/D' edges
    RETURN [v._key, e._key]
`);

Show output

[object ArangoQueryCursor, count: 4, results cached: false, hasMore: false]

[ 
  [ 
    "A", 
    null 
  ], 
  [ 
    "B", 
    "65565" 
  ], 
  [ 
    "C", 
    "65567" 
  ], 
  [ 
    "D", 
    "65569" 
  ] 
]

[object ArangoQueryCursor, count: 4, results cached: false, hasMore: false]

[ 
  [ 
    "A", 
    null 
  ], 
  [ 
    "B", 
    "65565" 
  ], 
  [ 
    "C", 
    "65567" 
  ], 
  [ 
    "D", 
    "65569" 
  ] 
]

You can see that expectations are fulfilled. You find the nodes in the correct ordering and the first edge is null, because no edge is pointing to the start node on this path.

You can also compute shortest paths based on documents found in collections:

db._query(`
  FOR a IN circles
    FILTER a._key == 'A'
    FOR d IN circles
      FILTER d._key == 'D'
      FOR v, e IN OUTBOUND SHORTEST_PATH a TO d GRAPH 'traversalGraph'
        RETURN [v._key, e._key]
`);

db._query(`
  FOR a IN circles
    FILTER a._key == 'A'
    FOR d IN circles
      FILTER d._key == 'D'
      FOR v, e IN OUTBOUND SHORTEST_PATH a TO d edges
        RETURN [v._key, e._key]
`);

Show output

[object ArangoQueryCursor, count: 4, results cached: false, hasMore: false]

[ 
  [ 
    "A", 
    null 
  ], 
  [ 
    "B", 
    "65565" 
  ], 
  [ 
    "C", 
    "65567" 
  ], 
  [ 
    "D", 
    "65569" 
  ] 
]

[object ArangoQueryCursor, count: 4, results cached: false, hasMore: false]

[ 
  [ 
    "A", 
    null 
  ], 
  [ 
    "B", 
    "65565" 
  ], 
  [ 
    "C", 
    "65567" 
  ], 
  [ 
    "D", 
    "65569" 
  ] 
]

And finally clean it up again:

var examples = require("@arangodb/graph-examples/example-graph");
examples.dropGraph("traversalGraph");

Show output

Empty Output